このページは「ARToolkit」のアルゴリズムを解析,解説していくページです.
歴史
ARマーカーを使った「ARToolkit」というものを考え,開発した人は,
2014年現在,奈良先端科学技術大学院大学で研究をされている加藤 博一教授です.[1]
そのため加藤のアルゴリズムとも呼ばれる「ARToolkit」の中身の原理について解説してみたいと思います.
基礎知識
カメラで撮影した画像に対して,空間的に正しい位置にAR表示をするためには,
カメラがARマーカーに対してどういった位置,姿勢にあるかがわかっていなければなりません.
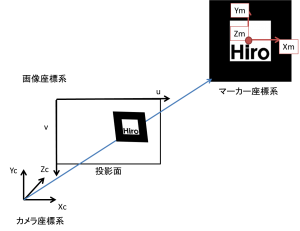
このアルゴリズムでは,マーカー座標系,カメラ座標系,画像座標系という3つの座標系を用います.
座標変換行列は,これらの座標系間を行き来するのに用いることができ,
それは座標系間の幾何学的な位置,姿勢関係を表しています.
正しい座標変換行列を計算することによって,空間的に正しい位置にAR表示をすることができます.
処理手順
- マーカーを2値化により認識
- 画像上でのマーカーの枠である4辺を計算する
- それぞれの辺を,カメラの投影方向に伸ばし,四角錐を作る
- 向かい合った面の交線ベクトルを求める
- 2つの交線ベクトルから,さらに外積を計算
- 平行移動成分を求める
※参考[2]
マーカーを用いたカメラの位置姿勢推定アルゴリズム
1.マーカーを2値化により認識
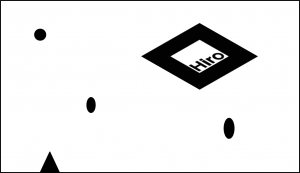
カメラから得られる画像を2値化(白黒画像化)し,その領域からマーカーの輪郭を検出します.
これについて詳しいアルゴリズムは,[3]を参照してください.
2.画像上でのマーカーの枠である4辺を計算する
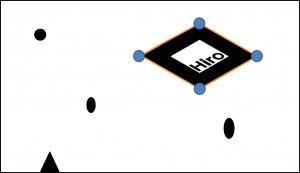
そこからマーカーの四角形の4辺の線分の式を求めます.
そして,4辺の交点,つまりマーカーの頂点を登録しておきます.
3.それぞれの辺を,カメラの投影方向に伸ばし,面を作る
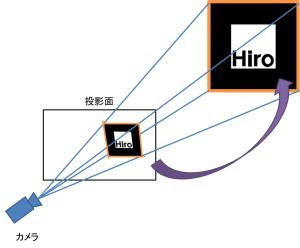
四角形の辺を取得したら,事前にカメラキャリブレーションによって得られた
カメラの内部パラメータ(CG空間上でのカメラの投影面までの距離など)を使って,
これらの辺とカメラの光学中心を結んだ面を作成します.
この面は実世界に置かれている3次元空間上のマーカーの4辺を通ることになるので,
カメラの光学中心,2次元画像上でのマーカーの辺,3次元上のマーカーの辺が含まれる面を4つ作ることになります.
4.向かい合った面の交線ベクトルを求める
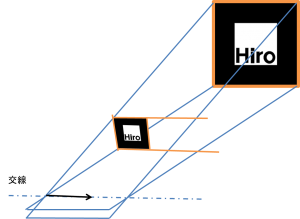
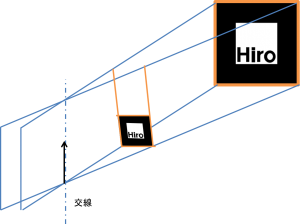
このように作った面の向かい合ったものどうしの交線を求めます.
交線の方向ベクトルは,2つの平面の法線ベクトルと垂直なベクトルであり,
この2つの法線ベクトルの外積によって求めることができます.[4]
また,マーカーの向かい合う辺が平行ならば,
この交線の方向ベクトルは,向かい合ったそれぞれの側面に対して平行なベクトルとなります.
つまり,マーカーの辺方向のベクトルを作ることができます.
5.2つの交線ベクトルから,さらに外積を計算
交線ベクトルからマーカーの辺方向のベクトルが2つ求まるので,
それらの外積を求めることで,マーカーの面に対して垂直な成分を作ることができます.
このようにすることで,マーカー座標系のX軸,Y軸,Z軸を求めることができ, マーカーの姿勢が推定できます.
辺方向のベクトルが必ず直交するということを証明しているのが[5]です.参考にしてください.
また,ここで画像処理の誤差により,交線ベクトルが互いに垂直でない場合には,
無理やり交線ベクトルが垂直になるように直しているようです.
6.平行移動成分を求める.
マーカー座標系の姿勢に関するパラメータ(回転,拡大縮小成分)を求めることができたので,
最後に平行移動成分を求めます.
マーカーの4つの頂点の画像座標上における位置と,マーカー座標系のおける位置との対応を使い,
平行移動成分を求めます.[6]
対応点から,2次元平面上でのx, yそれぞれについて,2 * 4 = 8つの式を得ることができるので,
そこから3つの未知変数で表される平行移動成分を求めることができます.
マーカーの制約
以上のアルゴリズムからマーカーは,
- 向かい合う二辺が必ず平行でなくてはならない.(平行四辺形 OK!,台形 NG!)
- CG空間の物体と実世界の間のスケールを同じにしたいならば辺の長さが既知でなくてはならない.(長方形でもOK)
という制約があると考えられます.
まとめ
通常,実世界の物体がカメラの画像上でどこにあるかといった座標変換行列(透視投影行列:P Matrix)を求める際には,
6組の実世界の3次元点と画像上の2次元点が必要であるが,
ARToolkitの場合,2次元のマーカーと2次元のカメラ画像座標のみで,
位置,姿勢関係を求めることができます.
2組の平行な辺があれば姿勢が求まるというアイディアは画期的なアイディアであり,AR以外の応用もできそうです.
参考文献
[1] Kato, H., Billinghurst, M. (1999) Marker Tracking and HMD Calibration for a video-based Augmented Reality Conferencing System. In Proceedings of the 2nd International Workshop on Augmented Reality (IWAR 99). October, San Francisco, USA.
[2] ARToolKitの解析 その① 変換行列の計算 – Pipe Render
http://render.s73.xrea.com/pipe_render/2008/04/artoolkit-12.html
[3] ARToolKitの解析 その② マーカーの認識 – Pipe Render
http://render.s73.xrea.com/pipe_render/2008/05/artoolkit-13.html
[4] 2平面の交線 http://www.hiramine.com/programming/graphics/3d_planeintersection.html
[5] マーカーでの姿勢認識 – やねうらお-俺のやねうら王がこんなに弱いわけがない。 (第2期) http://d.hatena.ne.jp/yaneurao/20100916
[6] 加藤博一, M. Billinghurst, 浅野浩一, 橘啓八郎,“マーカー追跡に基く拡張現実感システムとそのキャリブレーション”, 日本バーチャルリアリティ学会論文誌,Vol4, No4, pp.607-616, (1999)
